Како една равенка издлабена на мост во Даблин засекогаш ја промени математиката?

На 16 октомври 1843 година, ирскиот математичар Вилијам Роуан Хамилтон направил големо откритие додека шетал покрај Кралскиот канал во Даблин. Толку бил возбуден што го врежал своето откритие на мостот Брум:

i² = j² = k² = -1

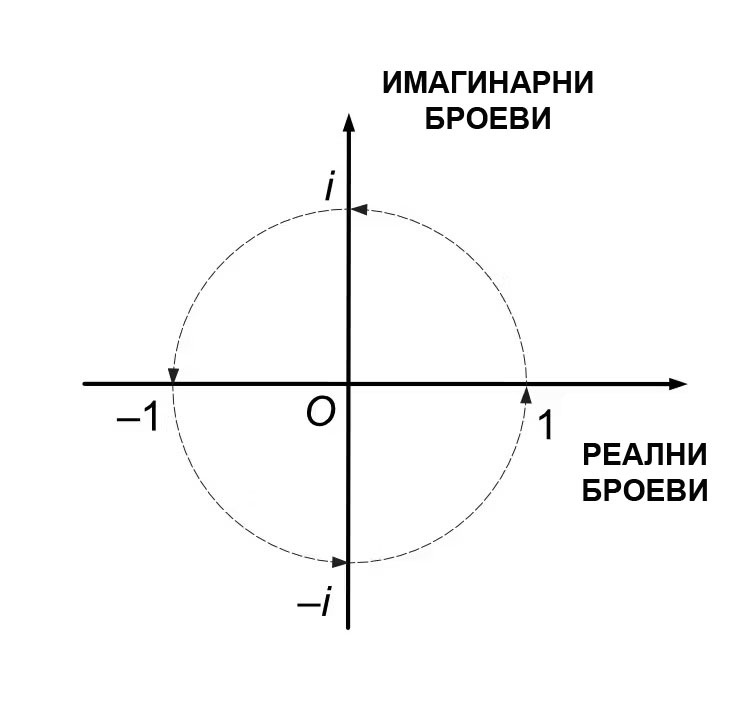
Ова откритие го променило начинот на кој математичарите ги претставуваат информациите, поедноставувајќи многу технички апликации, од пресметка на сили при дизајнирање мостови и уреди до програмирање на пребарувачи и ориентирање на ровери на Марс.

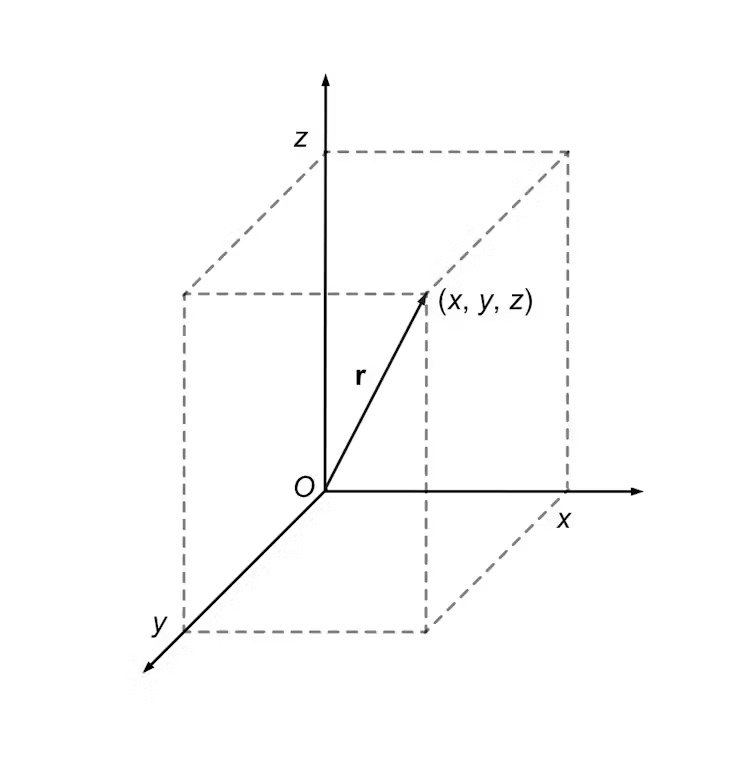
Хамилтон се обидувал да пронајде начин како да ги претстави ротациите во тродимензионален простор. Математичарите веќе знаеле како да ја претстават позицијата на објект со координати (x, y, z), но пресметувањето на ротациите било комплексно. Тој бил инспириран од комплексните броеви, кои користат реален и имагинарен дел, како i, каде i² = -1.

Хамилтон сакал да го прошири овој концепт во три димензии. По долги месеци размислување, сфатил дека му треба четиридимензионален простор со трета имагинарна оска k. Овие четиридимензионални броеви ги нарекол „кватерниони“ и ги користел за пресметка на ротации во 3D простор.

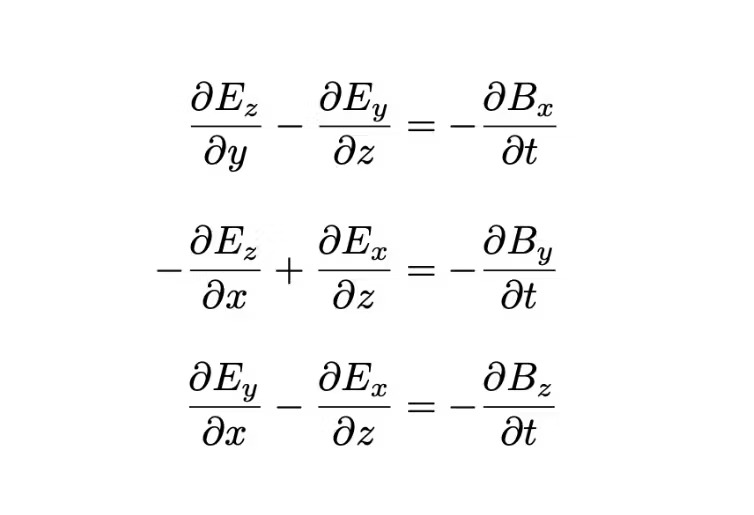
Најзначајниот дел од кватернионите е „векторот“, кој ги претставува големината и насоката на силите, брзините и други физички величини. Половина век подоцна, англискиот телеграфист Оливер Хевисајд го усовршил овој концепт, заменувајќи ги имагинарните оски со реални.

Ова откритие, и покрај првичниот отпор, подоцна добило признание од научната заедница, а векторите денес се користат во сè, од електроника до програмирање. Секоја година на 16 октомври, љубители на математиката го слават „Денот на Хамилтон“, одликувајќи го неговиот придонес.